Math er gal. Mens det grunnleggende er ganske enkelt, kan filosofien bak noen av de svært enkle grunnleggende være ganske dyp ... og til og med forvirrende. I dag skal vi se på alt fra primtal til uendelig. Så gjør deg klar fordi disse er 25 ekstraordinære matteprinsipper for å utfordre hjernen din!
Ekvatorrepet
 Kilde: abc.net.au, Bilde: pexels (offentlig domene)
Kilde: abc.net.au, Bilde: pexels (offentlig domene) Hvis du pakket et tau rundt jordens ekvator slik at det strammet jevnt på bakken, ville du bare måtte legge til ca 6, 3 meter tau for at hele greien skal hover 1 meter over bakkenivå (hele veien rundt Jord). Dette counterintuitive resultatet fungerer uansett hvor stor sfæren er. Den enkleste måten å forklare dette på er å huske at omkretsen er lik diameter ganger pi. Dette betyr at hvis du vil gjøre tauet 1 meter over jorden, trenger du bare å øke diameteren med 2 meter (1 meter på hver ende av kloden). Derfor trenger du bare å øke omkretsen av tauet med 2 x pi meter (6.28318530718 meter).
Hippasus av Metapontum
 Kilde: esoterx.com, Bilde: https://commons.wikimedia.org (offentlig domene)
Kilde: esoterx.com, Bilde: https://commons.wikimedia.org (offentlig domene) Mannen som viste at irrasjonelle tall eksisterte ble myrdet for det. Hans navn var Hippasus av Metapontum, og det skjedde rundt 520 f.Kr. Pythagoras og mange greske matematikere av tiden trodde at alle tallene var heltall, eller hele. Det var da Pythagoras utførte sine berømte trekantberegninger (Pythagoras teorem) at han snublet over kvadratroten av to. For å lage en lang historie kort, forsøkte han å forsøke å holde sin hemmelighet og vendt ut da Hippasus publiserte det.
Munchausen tall
 Kilde: zach.se
Kilde: zach.se Bortsett fra å gjøre noen forutsetninger om 0 ^ 0, er 3435 det eneste nummeret i tillegg til 1 hvor du kan dele hvert siffer opp, heve det til egen kraft, summere alt sammen, og få samme nummer tilbake. I utgangspunktet fungerer 3 ^ 3 + 4 ^ 4 + 3 ^ 3 + 5 ^ 5 = 3435 Merk: 438579088 fungerer også hvis du antar at 0 ^ 0 = 0. Disse kalles Munchausen tall.
Desimalrepresentasjonen av 7. s
 Bilde: https://pixabay.com (offentlig domene)
Bilde: https://pixabay.com (offentlig domene) Desimalrepresentasjonene av 7. er det samme settet med tall som gjentas, bortsett fra alltid å starte fra et annet punkt. 1/7 = 0.142857142857 ... og 2/7 = 0.285714285714 ... og 3/7 = 0.428571428571 ...
Binær finger telling
 Kilde: mathisfun.com, Bilde: https://pixabay.com (offentlig domene)
Kilde: mathisfun.com, Bilde: https://pixabay.com (offentlig domene) Hvis du bruker binær, kan du telle til 1023 på fingrene.
10!
 Kilde: reddit.com
Kilde: reddit.com Det er akkurat 10! sekunder om 6 uker. Det er lettere å se dette når du bryter det ned som sådan: 6 * 7 * 24 * 60 * 60 = 6 * 7 * (8 * 3) * (3 * 2 * 10) * (1 * 3 * 4 * 5) = 6 * 7 * 8 * 9 * 2 * 10 * 1 * 3 * 4 * 5 = 10!
Grahams nummer
 Kilde: ibmathresources.com, Bilde: https://pixabay.com (offentlig domene)
Kilde: ibmathresources.com, Bilde: https://pixabay.com (offentlig domene) Grahams tall er så stort at hvis du skrev hvert siffer så lite som mulig, ville det fortsatt ta opp mer plass enn det er tilgjengelig i det observerbare universet. Faktisk, hvis du kunne holde alle sifrene i hodet ditt, ville hjernen kollapse inn i et svart hull (på grunn av den astronomiske tettheten av nevrale forbindelser du ville trenge).
Gjentatte decimaler
 Bilde: https://pixabay.com (offentlig domene)
Bilde: https://pixabay.com (offentlig domene) Eventuelle repeterende desimaler kan skrives som en brøkdel over et tilsvarende antall 9-tall (som den gjentatte delen). For eksempel vil .456456456 ... være 456/999
Shuffling kort
 Kilde: qi.com, Bilde: https://www.pexels.com (offentlig domene)
Kilde: qi.com, Bilde: https://www.pexels.com (offentlig domene) Hver gang du tilfeldigvis blander et dekk med 52 kort, har du nesten sikkert arrangert dem i en helt unik rekkefølge. Det vi mener med dette er at i hele menneskehetens historie har ingen noen gang spilt et dekk på samme måte. Hvordan? Vel, det er 52! måter du kan bestille dekk på (52 * 51 * 50 ...) Dette fører til 8.0658 x 10 ^ 67 muligheter. Til sammenligning er universet bare 1 x 10 ^ 18 sekunder gammelt. Selv om du blandet ett dekk hvert sekund siden big bang ... vil du fortsatt falle kortvarig kort.
Den lille flasken
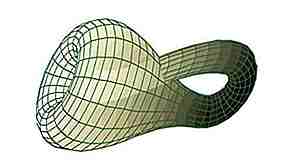 Kilde: math.union.edu
Kilde: math.union.edu Hvis du tar to Möbius striper og strekker kantene slik at de knytter sammen (i virkeligheten limer dem sammen), lager du en Klein Bottle. Denne "flasken" er et eksempel på en ikke-orienterbar overflate. I utgangspunktet eksisterer den bare i 4 dimensjoner, men kan løst representeres i 3. Som Möbius-stripen har den bare 1 overflate, men ingen kanter. Det er ganske trippy.
Frivillig teorem av aritmetikk
 Kilde: mathworld.wolfram.com, Bilde: https://pixabay.com (offentlig domene)
Kilde: mathworld.wolfram.com, Bilde: https://pixabay.com (offentlig domene) Den frivillige teorem av aritmetikk sier at på grunn av å være uendelig, er det store flertallet av naturlige tall veldig, veldig store.
Hva ligger mellom 0 og 1

Det er en uendelig mengde tall mellom 0 og 1 (og 1 og 2, osv.). For eksempel, ½, ⅓, ¼, og du kan bare fortsette å gå.
Ikke-beregnet tall
 Kilde: igoro.com, Bilde: http://www.pixnio.com (offentlig domene)
Kilde: igoro.com, Bilde: http://www.pixnio.com (offentlig domene) Nesten alle reelle tall er irrasjonelle. Enda mer, de fleste irrasjonelle tallene er ikke engang beregnbare. Og for å virkelig skryte ditt sinn, er hvert enkelt tall du noensinne har sett i ditt liv, beregnet, inkludert uendelig gjentatte tall som pi (fordi du kan lage en algoritme for å beregne det). Så, for å sette ting helt enkelt, er det en uendelig mengde tall der ute som vi aldri vil se (faktisk ... de fleste) fordi vi ikke har mulighet til å beregne disse tallene. På en eller annen måte er de "matematikkens" mørke materie. Vi vet at de er der og at de utgjør det uutslettelige flertallet av tall, men vi har ingen måte å nå dem. Merk: Chaitins konstant er et eksempel på ikke-beregnbart nummer, men dessverre ... det er ikke beregnet.
De forskjellige typer uendelig
 Kilde: math.brown.edu, Bilde: https://pixabay.com (offentlig domene)
Kilde: math.brown.edu, Bilde: https://pixabay.com (offentlig domene) Selv om heltallene er uendelige, er det uendelig mer reelle tall enn heltall. Hvordan kan det være hvis heltallene allerede er uendelige? Det er fordi det er to typer uendelig ... tellerbare og utallige. Heltall er uendelig tellbare, mens ekte tall ikke er (fordi de også inneholder irrasjonelle tall). Så dette fører til noen vanlige konklusjoner. Antall positive heltal (0, 1, 2, ...) er nøyaktig det samme som antall positive og negative heltall kombinert (..., -3, -2, -1, 0, 1, 2, 3, ...). Selv om disse to uendelige settene er like, er de begge mindre enn det uendelige sett med ekte tall. Faktisk er det uendelig flere tall mellom bare to tilfeldige heltall (0 og 1 for eksempel) enn det er i hele uendelige sett med heltall!
De vanlige tallene
 Kilde: mathworld.wolfram.com
Kilde: mathworld.wolfram.com Et normalt tall er i utgangspunktet et irrasjonelt tall som ikke har noe mer av et gitt tall enn en annen. Så for eksempel i tallet 4.56856948576434 ... skal hvert siffer vises omtrent like mange ganger helt ut til uendelig. Selv om det er grovt bevis for å vise at de fleste reelle tallene er normale, og vi mistenker at tall som pi og e er normale, har vi fremdeles ikke kunnet vise det.
De transcendentale tallene
 Kilde: mathworld.wolfram.com
Kilde: mathworld.wolfram.com Selv om nesten hvert eneste virkelige og komplekse tall er transcendentalt (i motsetning til algebraisk, som egentlig er et tall som er roten til et polynom), er det bare noen få som er kjent, først og fremst fordi det er veldig vanskelig å bevise at et tall er transcendentalt. De mest kjente transcendentale tallene er e og pi.
Den ensomme prime
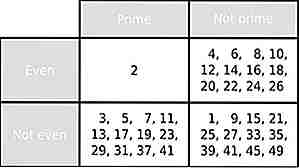 Kilde: mathworld.wolfram.com, Bilde: https://commons.wikimedia.org (offentlig domene)
Kilde: mathworld.wolfram.com, Bilde: https://commons.wikimedia.org (offentlig domene) Hvert enkelt primallall helt gjennom til uendelig er merkelig. Bortsett fra 2.
Effekten av uendelig på sannsynligheten
 Bilde: https://pixabay.com (offentlig domene)
Bilde: https://pixabay.com (offentlig domene) Begrepet uendelig har noen galte virkninger på sannsynligheten. Hvis du skulle tilfeldig velge et ekte tall, er sannsynligheten for at det er rasjonelt (1, 2, ¾, 78/56, ...) 0. Dette går tilbake til det faktum at irrasjonelle tall er uendelig uendelig, mens de rasjonelle tallene er teltvis uendelig. Og tellerbar uendelighet over uendelig uendelighet er 0.
.999 ... = 1
 Bilde: https://commons.wikimedia.org (offentlig domene)
Bilde: https://commons.wikimedia.org (offentlig domene) .999 ... er lik 1. Ved dette punktet er tankene dine så sannsynligvis så prangende med begrepet uendelig at du sannsynligvis bare vil akseptere det vi forteller deg, men vi vil bevise det. Du vet at .333 ... er lik ⅓ og .666 ... er lik ⅔. ⅓ + ⅔ = 1 og .333 ... + .666 ... = .999 .... En annen måte å tenke på dette er at hvis .999 ... ikke er lik 1, må det være noen tall mellom .999 ... og 1. Som, takket være begrepet uendelig, er det ikke.
Dirichlet-funksjonen
 Kilde: mathworld.wolfram.com
Kilde: mathworld.wolfram.com Ifølge Dirichlet-funksjonen, mellom noen irrasjonelle tall er det et rasjonelt tall. Den galne delen? Det er uendelig flere irrasjonelle tall enn rasjonelle tall (som vi tidligere har etablert). Så ... hvordan kan hvert irrasjonelt tall ha et rasjonelt tall mellom dem? Du forventer å gå tom for rasjonelle tall. Men uendelighet oppfører seg ikke slik vi forventer det.
Eulers identitet
 Kilde: mathworld.wolfram.com
Kilde: mathworld.wolfram.com Eulers identitet er ofte sitert som et eksempel på matematisk skjønnhet. Det er e ^ (pi * i) + 1 = 0. Den inneholder 5 av de mest grunnleggende matematiske konstantene 0, 1, e, pi og i. Tre av de grunnleggende aritmetiske operasjonene opptrer også nøyaktig en gang: tillegg, multiplikasjon og eksponering. Benjamin Peirce, en kjent matematiker en gang sa etter å ha bevist det i et foredrag, "identiteten er helt paradoksal; vi kan ikke forstå det, og vi vet ikke hva det betyr, men vi har bevist det, og derfor vet vi at det må være sannheten. "
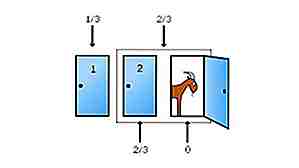
Monty Hall Problem
 Kilde: mathworld.wolfram.com, Bilde: https://commons.wikimedia.org (offentlig domene)
Kilde: mathworld.wolfram.com, Bilde: https://commons.wikimedia.org (offentlig domene) Monty Hall-problemet er et kjent eksempel på hvor sannsynligheten kan være mot-intuitiv. La oss si at på et spill viser er det tre dører. Bak en av dem er en bil mens de to andre gjemmer geiter. Du velger å åpne dør 1. Verten vet imidlertid hva som ligger bak dørene. Han åpner dør 3 for å avsløre en geit. Nå spør han om du vil endre ditt valg til dør 2. Hva gjør du? Svaret er at du bør endre ditt valg. Hvorfor? Fordi ved å bytte til dør 2 du har ⅔ sjanse til å vinne bilen mens du bor på døren 1 har du omtrent en sjanse. Den beste måten å visualisere denne motintuitive løsningen på er å øke antall dører. La oss si nå at det er 100 dører. Du velger dør 37. Verten åpner nå alle dørene for å avsløre geiter med unntak av dør 83. Ønsker du å endre valget fra 37 til 83? Eller vil du bli på 37? Faktum er at sjansene dine for å vinne bilen vil øke betydelig ved å bytte til dør 83.
Forskjellen mellom 1 million og 1 milliard

En million sekunder er omtrent 11 og en halv dag. En milliard sekunder er like under 32 år.
The Pigeonhole Principle
 Kilde: mathworld.wolfram.com, Bilde: https://commons.wikimedia.org (offentlig domene)
Kilde: mathworld.wolfram.com, Bilde: https://commons.wikimedia.org (offentlig domene) Hvis du har 2 typer sokker i skuffen din og du tilfeldigvis griper 3 uten å se, er du garantert å ha et matchende par. Mens for noen mennesker er dette åpenbart, for andre kan det være vanskeligere å forstå. Det er basert på noe som heter pigeonhole-prinsippet. I utgangspunktet, hvis du har n typer noe, må du tilfeldig velge n + 1 for det for å få en kamp. Så, hvis du har 5 forskjellige typer sokker i skuffen din og du tilfeldigvis tar 6 av dem ... er du garantert å ha en kamp. Dette kan være bra for å bli kledd i mørket!
Summen av alle positive heltall fra 1 til uendelig
 Kilde: se nedenfor, Bilde: https://commons.wikimedia.org (offentlig domene)
Kilde: se nedenfor, Bilde: https://commons.wikimedia.org (offentlig domene) Nå, gjør deg klar for muligens den mest slemme tingen du noen gang kommer til å høre i hele livet ditt. Hvis du legger opp alle de positive heltalene fra 1 til uendelig ... hva får du? Gikk du til -1/12? Fordi det er det riktige svaret. Vi vet. Dette høres helt latterlig ut og i noen grad er det. Hvorfor? Fordi å legge noe opp til uendelig er det umulig og sikkert å gi latterlige resultater. For å gjøre ting enda mer spennende for deg, er dette resultatet faktisk veldig godt kjent i fysikk, spesielt strengteori. Faktisk, hvis du fortsatt ikke kan tro på dette, foreslår vi at du ser på denne videoen av fysikere Tony Padilla og Ed Copeland fra University of Nottingham. De forklarer galskapen bedre enn vi kan - https://www.youtube.com/watch?v=w-I6XTVZXww.
Merk: Resultatet stammer i stor grad fra det faktum at uendelig tåler våre forventninger. Infinity er ikke et tall, det er et konsept. Ting som tillegg og subtraksjon virker ikke det samme når du involverer uendelig (slags fysikk fungerer ikke det samme når du står midt i et svart hull).
Mer informasjon: Det er også verdt å se på Ramanujan-summeringen og Grandi-serien:
https://en.wikipedia.org/wiki/Ramanujan_summation
https://en.wikipedia.org/wiki/Grandi's_series
En annen ressurs:
http://www.bradyharanblog.com/blog/2015/1/11/this-blog-probably-wont-help
Bilder: Utvalgt bilde: https://commons.wikimedia.org (offentlig domene), 20. maks pixel, 16. Tttrung, Klein bottle2, CC BY-SA 4, 0, 11. Mehran Moghtadaei, PP 1280 × 1024, CC BY- SA 3.0, 10. Stephen J. Brooks (talk), Algebraicszoom, CC BY 3.0, 6. Judy Breck via flickr, CC BY-SA 2.0, 5. Quinn Dombrowski fra Chicago, USA, Eulers Identity Graffito, CC BY-SA 2.0, 3. Cmglee, Visualisering 1 milliard, CC BY-SA 3.0,




