25 enkle mentale matte triks som vil blåse deg i sinnet

For å se om et tall er delbart med tre, legg til tallene. Hvis summen er delt med tre, så er tallet. Merk: Dette fungerer også for 9.

x% av y er det samme som y% av x. Dette betyr at hvis 2% av 50 er for vanskelig å finne ut, kan du bare vende den - 50% av 2. Det er mye enklere.

Hvis du vil multiplisere et 2-sifret tall med 11, legger du bare til tallene sammen og holder svaret mellom dem. For eksempel vil 42 * 11 være 4 + 2 = 6. Sett nå 6 mellom 4 og 2 for å få 462.

Merk: Ikke glem å bære 1. For å gi et annet eksempel, vil 58 * 11 være 5 + 8 = 13. Du kan ikke bare sette 13 mellom 5 og 8 skjønt. Det ville gi 5138, som er åpenbart feil. Du må bære den ved å legge den til 5. Så det ville være 638.

Hvis du må multiplisere et tall med 5, kan det være lettere å halve det og deretter multiplisere med 10. For eksempel vil 315 * 5 være 315/2 = 157.5 Nå bare flytte desimal over til å multiplisere med 10 og få 1575.

For å tilnærme en kvadratrot, gjør du følgende. Finn neste lavere perfekte firkant. Legg det til nummeret ditt. Nå deles av kvadratroten til den nedre perfekte firkanten. Og nå dele igjen med 2. Lyder det hardt? Her er et eksempel. Ta 31. Den nest laveste perfekte firkanten er 25. Så 31 pluss 25 er 56. Del nå med kvadratroten på 25. Så 56/5 = 11.2 Del nå med 2 for å få 5.6

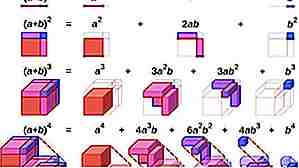
Bruk binomialteoremet (a + b) ^ 2 = a ^ 2 + 2ab + b ^ 2 til firkantede tall. For eksempel kan 55 ^ 2 være (50 + 5) ^ 2. Dette betyr at 50 * 50 + 50 * 5 * 2 + 5 * 5 = 2500 + 500 + 25 = 3025.

For å se om et tall er delt med 8, sjekk de tre siste sifrene. Hvis de er delbare med 8, er tallet delbart med 8. For eksempel ville 3423024 være delbart med 8 fordi 024/8 = 3

For å finne et tips bare flytte desimal ett sted til venstre for å få 10%. Deretter legger du halvparten av det du har igjen for å få 15% eller dobler den for 20%. For eksempel, hvis regningen er $ 43, 21 så $ 4, 32 er 10%. Halvparten av $ 4, 32 er $ 2, 16, så hvis du vil ha 15% bare legg til det på. Det ville gi deg $ 4, 32 + $ 2, 16 = $ 6, 48. Å få 20% er enda enklere fordi du bare dobler den. $ 4, 32 * 2 = $ 8, 64. Så hvis du føler deg generøs da vil $ 8, 64 utgjøre en 20% tips.

For å beregne årslønn, bare ta din timelønn, doble den og legg til 3 nuller. La oss si at du lager $ 8 per time. Bare doble det for $ 16 og legg deretter til tre nuller for $ 16.000.

Til omtrentlige konverteringer mellom Celsius og Fahrenheit bare multipliser med 2 og legg til 30 (går fra C til F). Gjør omvendt for å gå fra F til C (trekke 30 og del med 2).

For å se om et tall er delt med 4, se bare de to siste sifrene. Hvis de er delbare med 4, er hele tallet delbart med 4. Så 23746316 vil være delelig med 4 fordi 16 er delt med 4.

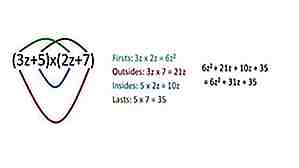
For å multiplisere to tall sammen, bruk FOIL-metoden (først, ytre, indre, siste). For eksempel vil 25 * 37 være (20) (30) + (5) (30) + (7) (20) + (5) (7) = 925.

Merk: Dette er akkurat det du gjør når du multipliserer på papir, det er bare enklere å visualisere FOIL-metoden i hodet ditt.

For å beregne prosentandelen av et tall (det er ikke 10%), finn bare 1% først og multipliser det deretter. Så, for eksempel, ville 3% av 528 være 528 * .01 = 5, 28 (flytte desimal to plasser igjen). Nå bare multipliser med 3 for å få 15.84

Dette fungerer spesielt godt hvis en av tallene allerede er fin og rund (slutter med 0). Bare runde av det andre nummeret, multipliser, og juster resultatet tilsvarende. For eksempel, hvis du vil beregne 18 * 30, trenger du ikke FOIL-metoden vi gjorde tidligere (fordi 30 er allerede fin og rund). Bare gjør 20 * 30 som er 600 og trekker deretter to 30s for 540.

For å sjekke om et nummer er delt med 6, må du kombinere to delbarhetsregler (to og tre år). Hvis det er delbart med både 2 og 3, så er det delbart med 6. Vi gjorde delbarhet med 3 allerede, men bare i tilfelle ... like tall er delbare med 2.

Desimalrepresentasjonen av 11. kan gjøres ved å multiplisere telleren med 9 og bare gjenta det. For eksempel, 1/11 = .09090909 .... og 2/11 = .18181818 ... etc

For å firkantet et dobbeltsifret tall som slutter i 5, sett bare 25 på slutten og multipliser det første tallet med følgende siffer. Så for eksempel vil 45 ^ 2 være 2025 fordi 5 er det neste tallet over 4 så 4 * 5 = 20. Legg bare en 25 på slutten for 2025.

Desimalrepresentasjonene for niende er bare telleren gjentatt. For eksempel 1/9 = .1111111 ... og 2/9 = .2222222 ... Dette er også et av bevisene som brukes til å vise det .999999 ... = 1. (siden 9/9 = .99999 ...)

For kvadreringsnumre er et mulig triks å legge til / trekke fra tallet til du får to tall du enkelt kan multiplisere. Deretter legger du til forskjellen på tallet du har lagt til / trukket fra. For å gi et eksempel, kan 46 ^ 2 være 42 * 50 fordi 46 - 4 = 42 og 46 + 4 = 50. Så 42 * 50 vil være 2100. Nå kvadrat nummeret du la til / trekk så 4 ^ 2 = 16. Nå legg til 16 for å få 2116.

72 delt med renten vil gi deg et grovt anslag på hvor mange år det ville ta å fordoble pengene dine (regel 72).

For å gjøre mentalt tillegg, er det mye lettere å jobbe fra venstre til høyre enn på måten du gjør på papir (høyre til venstre). Dette skyldes at hjernen din naturligvis gjenkjenner og husker tall som starter til venstre. For eksempel å gjøre 376 + 581, legg til 300 + 500 for å få 800. Legg nå på 70 + 80, som er 150. Dette gir totalt til 950. Deretter legger du på 7 for å få 957. I utgangspunktet bryter du tillegget ned inn i mindre deler fra venstre til høyre. En annen fordel med dette er at du gradvis kommer inn på løsningen. Så, hvis du bare vil ha en tilnærming, behøver du ikke vente til du er ferdig med problemet, for å finne ut hvilken størrelsesorden du arbeider med (hundrevis, tusenvis osv.)

For mental subtraksjon, er ideen likt til tillegg. Arbeid fra venstre til høyre, men det er et ekstra knep som du må være oppmerksom på (hint: det innebærer avrunding). La oss si at du vil gjøre 632 - 487. Først legg til 3 for å runde 487 til nærmeste 10, så 490. Nå blir problemet 632-490. Dette er mye lettere. 632-400 er 232. Nå trekker du 90 du får 142 (det er 10 mer enn å trekke 100). Derfra, husk å legge tilbake 3 fra begynnelsen. Dette gir deg 145.

Et annet triks for å multiplisere tall som enkelt avrundes (vanligvis slutter i 8 eller 9), er å bruke subtraksjonsmetoden. For å gjøre dette, ringer du opp nummeret og trekker deretter av. For eksempel ville 49 * 16 være 50 * 16. Dette er mye enklere å løse. Siden 100 * 16 er 1600, kan du halve det for å få 800. Husk nå å trekke fra det du avrundet. Så, siden du avrundet 49 opp til 50, var det 1 * 16, som er det du må trekke fra. Det gir 800 - 16 som er 784.

Husk at du kan gjøre alt du vil ha en ligning så lenge du gjør det til begge sider. Også, du kan gjøre hva du vil til et begrep, så lenge du multipliserer det med en. Husk at 1 har uendelige former (2/2, (x-4) / (x-4), osv.).

For å konvertere mil til kilometer, kan du få et pent nært estimat ved å legge til 60%. Den raskeste måten å gjøre dette på er å legge til 50% og deretter 10%. For eksempel. 60 miles i km ville være følgende: 60 * .5 = 30 og 60 * .1 = 6. Nå, 30 + 6 = 36. Legg dette til 60 for å få 96 km. Å trekke fra kilometer til miles, bare trekke 40%. Du kan gjøre dette ved å trekke 50% og deretter legge til 10%. Så for å få 350 km i miles trekker halvparten av 350. Det gir deg 175. Nå legger du tilbake 10% av 350 som er 35. Dette gir deg 210. Merk: Husk at disse er svært grove estimater. Jo større tallene dine blir, jo mer feil blir det.